Úvod
Nejprve si v pythonu napíšu kód pro sestavení základní neuronové sítě, na které budu ilustrovat základní myšlenky jejich stavby a funkce
Základní schéma neuronové sítě, normalizační funkce
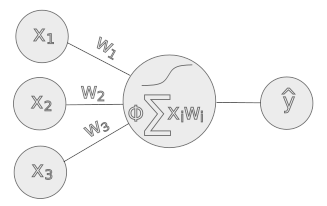
Neuronová síť se zkládá ze vstupů, synapsí, neuronů a výstupů.
V mém příkladu budu mít 3 vstupy, 1 neuron a 1 výstup
Hodnota daného neuronu je sumou násobků vstupu a jeho váhy. Na tuto sumu aplikujeme normalizační funkci (Sigmoid).
$$ \sum_{i=1}^{3}x_i w_i = x_1 w_1 + x_2 w_2 + x_3 w_3 $$
Aplikace normalizační funkce Sigmoid.
$$ \phi(\sum_{i=1}^{3}x_i w_i) $$
$$ \phi(x) = \frac{1}{1+e^{-x}} \rightarrow \phi(x) = \frac{1}{1+e^{-\sum_{i=1}^{3}x_i w_i)}} $$
Normalizační fuknce vrací hodnotu mezi 0 a 1
Trénovací proces
- Použijeme vstupy z trénovacích dat a necháme vygenerovat výstup na základě náhodně iniciovaných vah jednotlivých synapsí.1. Použijeme vstupy z trénovacích dat a necháme vygenerovat výstup na základě náhodně iniciovaných vah jednotlivých synapsí.
- Vypočítáme chybu, která je rozdílem mezi skutečným výstupem a vygenerovaným výstupem.
- V závislosti na velikosti chyby nastavíme v dalším kroku nové hodnoty vah synapsí.
- Tento ostup opakujeme např. 20.000 krát.
Zpětná propagace
Nastavení váhy synapse = chyba x vstup x $\phi$'(výstup)
Chyba = výstup – vypočtený výstup
Vstup = buď 1 nebo 0
$$ \phi(x) = \frac{1}{1+e^{-x}} \rightarrow \phi'(x) = \phi(x).(1 – \phi(x)) $$
Z tohoto vztahu vyplývá, že derivace normalizační fuknce sigmoid nám určuje rychlost změny dané váhy (tečna v daném bodě funkce). Pokud je výstup vysoké kladné nebo záporné číslo, znamená to, že neuron si je jistý ve svém odhadu a váhá již není tolik korigována. Naopak v případě nízkých hodnot okolo nuly, je rychlost změny velká, což značí velkou nejistotu a tyto váhy musejí být adekvátně přenastaveny. Toto přenastavení nazýváme zpětná propagace.
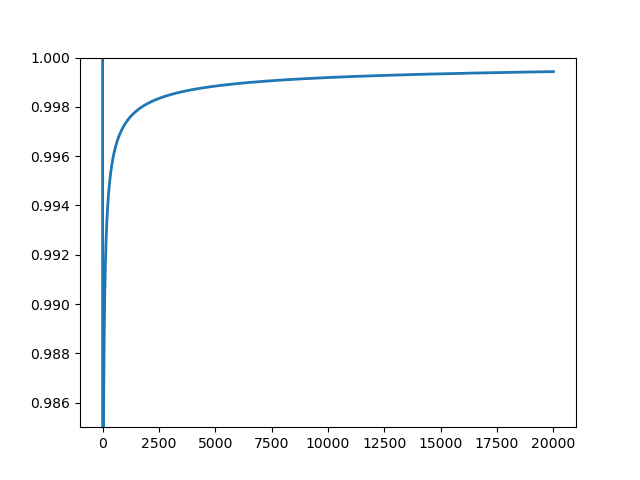
Grafické znázornění postupné korekce chyby neuronové sítě v průběhu 20.000 iterací zpětné propagace.
