Konvergence a CFL podmínka
V předchozích dvou krocích jsme aproximovali lineární a nelineární konvekci. V obou případech bylo potřeba okrajové podmínky nastavit tak, aby propagace funkce nedivergovala a zachovala co nejvíce svou charakteristiku.
V tomto kroce za pomocí CFL čísla (Courant-Fridrichs-Lewy) ověříme stabilitu výpočtu. Toto číslo je nezbytnou podmínkou pro konvergenci při numerickém řešení parciálních diferenciálních rovnic. Vzniká při numerické analýze explicitních schémat časové integrace, kdy jsou použita tato numerická řešení.(Wikipedia)
Pro ukázku vlivu okrajových podmínek na CFL číslo použijeme znovu kód z prvního kroku pro lineární konvekci.
Zde jsou původní okrajové podmínky, postupně budeme zvyšovat zajemnění sítě a budeme pozorovat, jak se bude funkce chovat:
nx=41 #number of grid points
dx=2/(nx-1) #distance between adjacent points
dt=0.025 #time of each timestep
nt=20 #number of timesteps
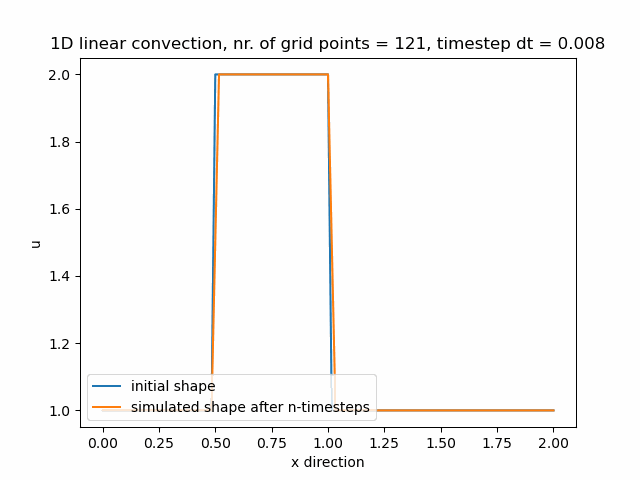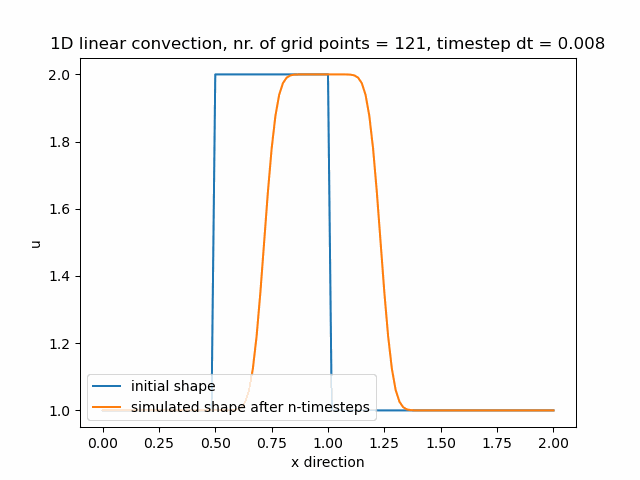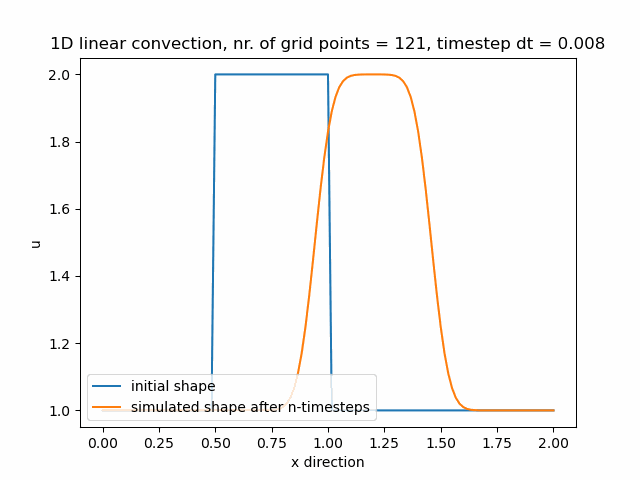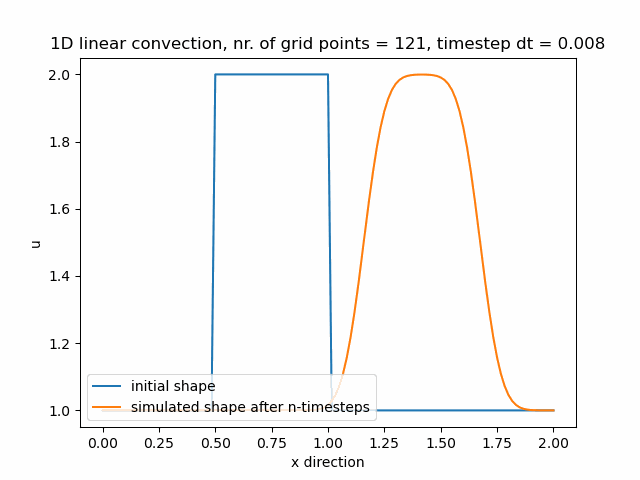
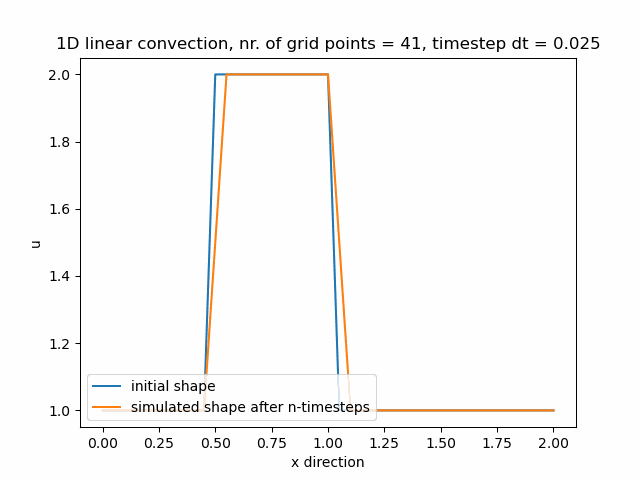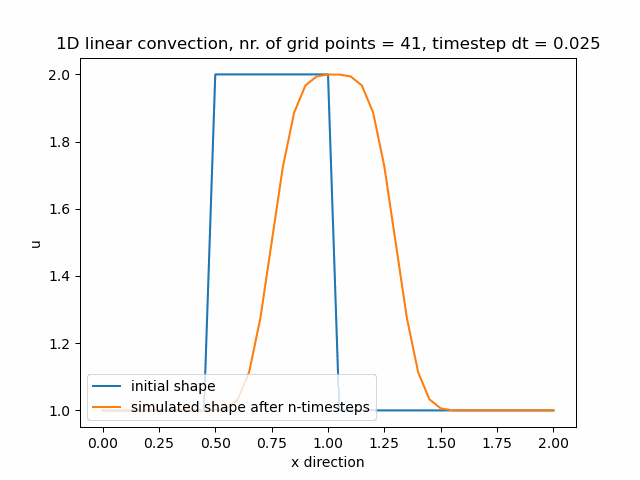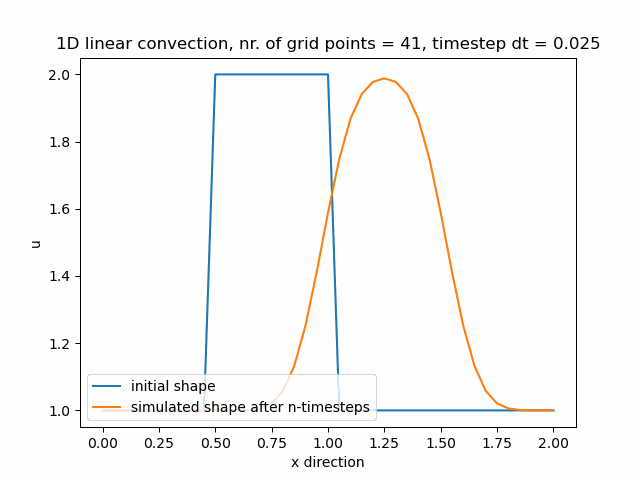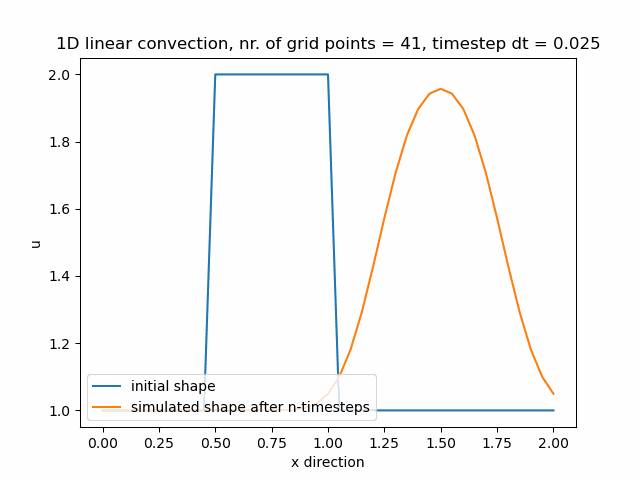
c=1 #wave speedPrůběh funkce pro nx=41, zde je stále velká numerická difuze.
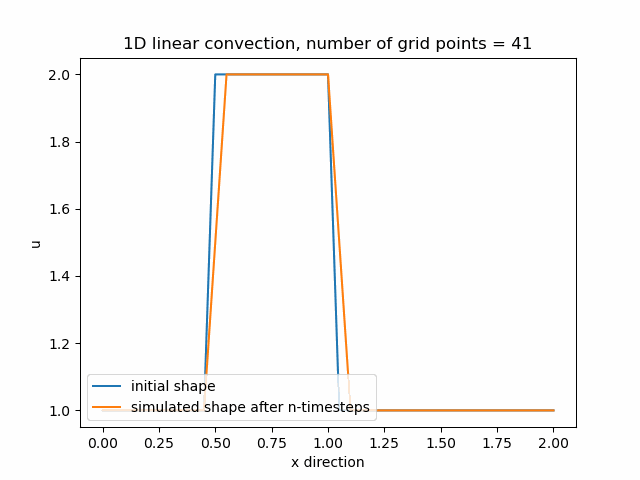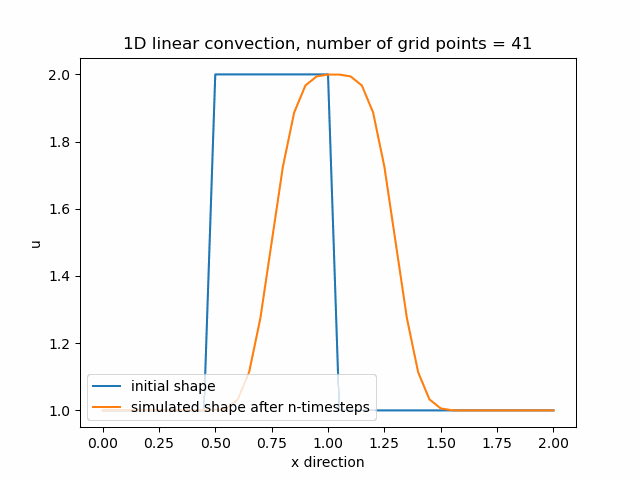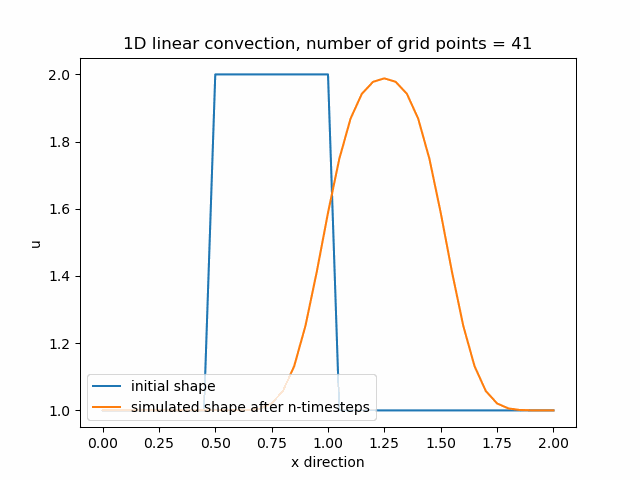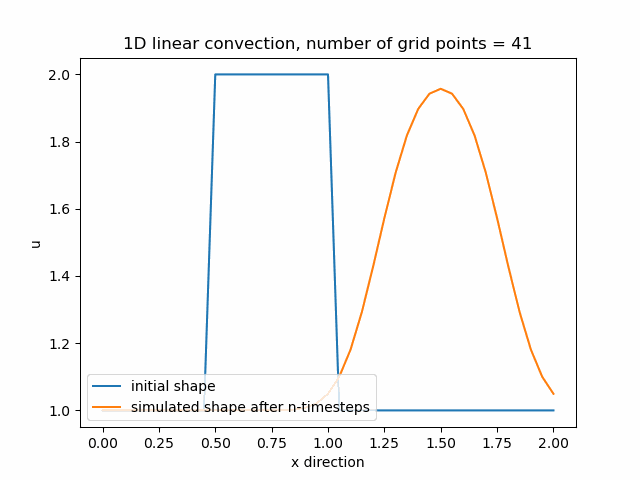
Průběh funkce pro nx=61, difuze je stále znatelná.
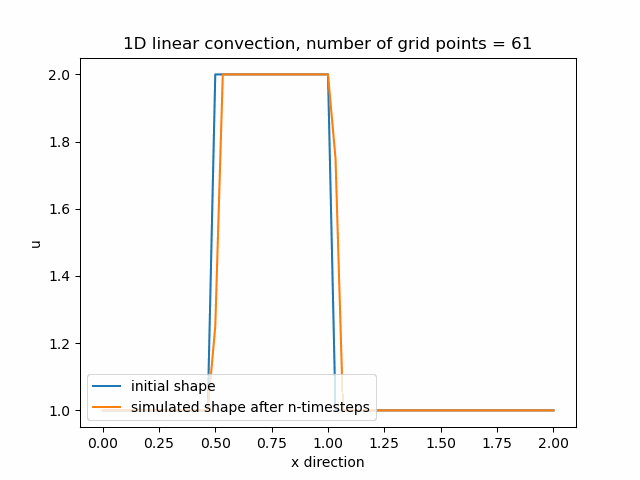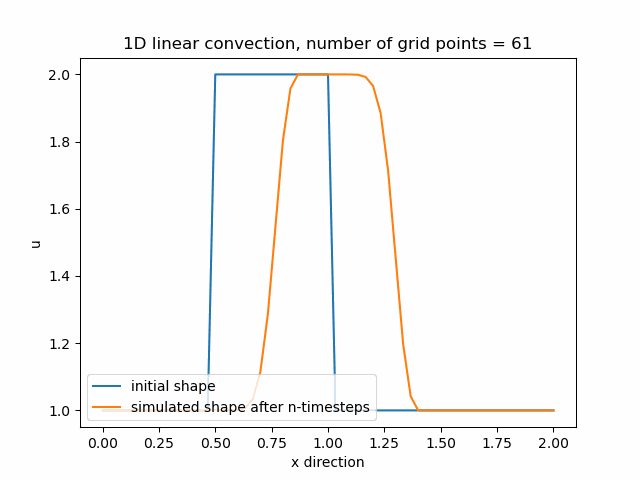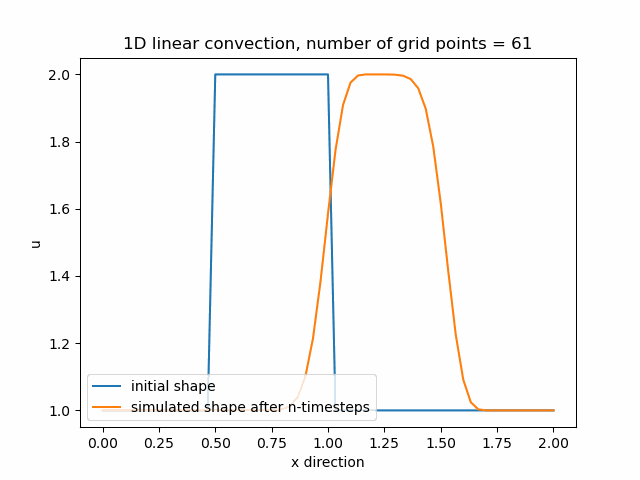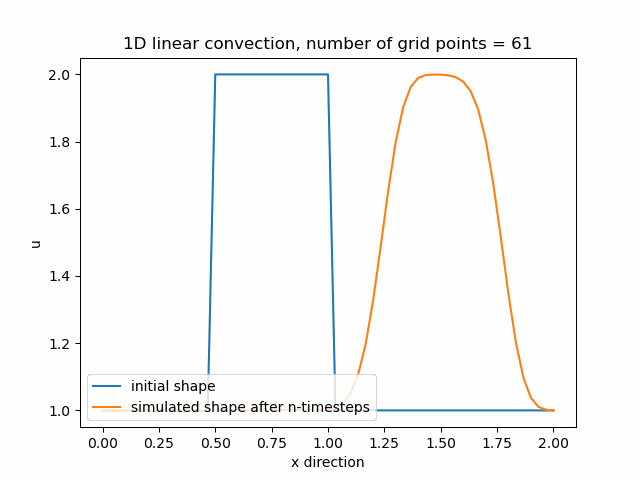
Průběh funkce pro nx=71, nyní se již funkce začíná přibližovat svému původnímu tvaru.
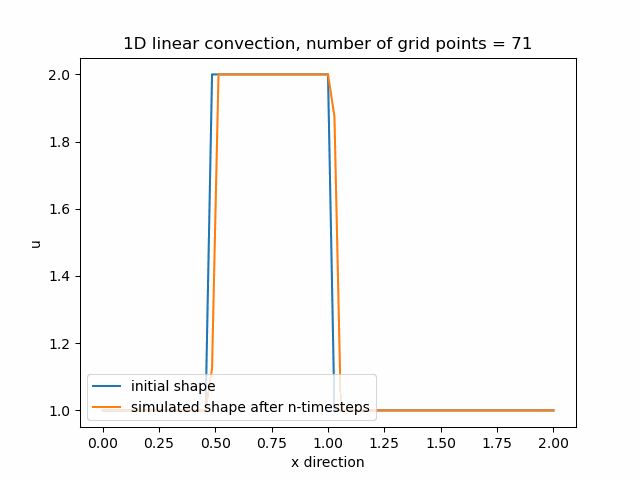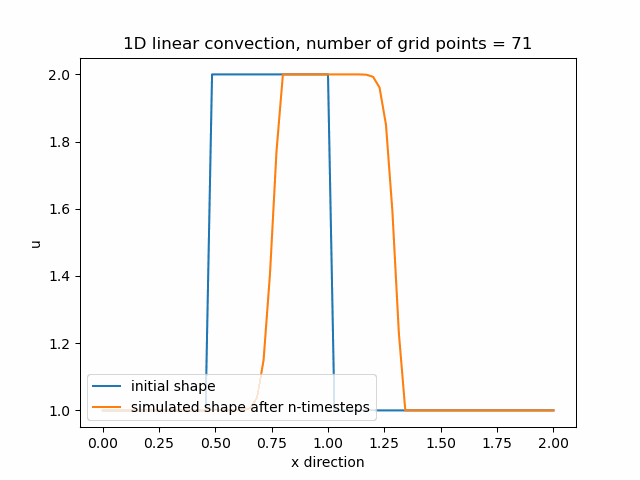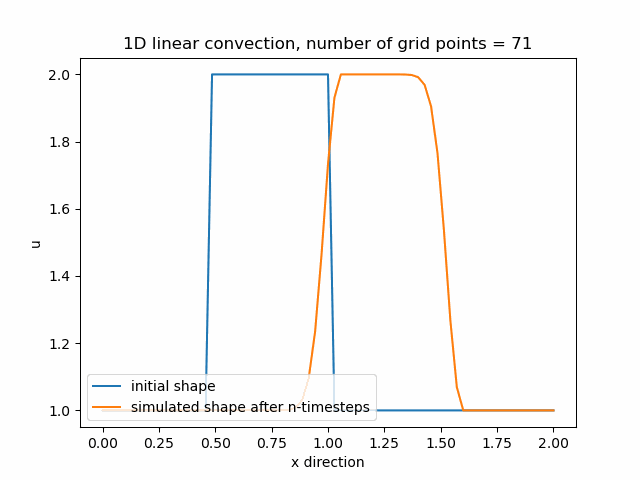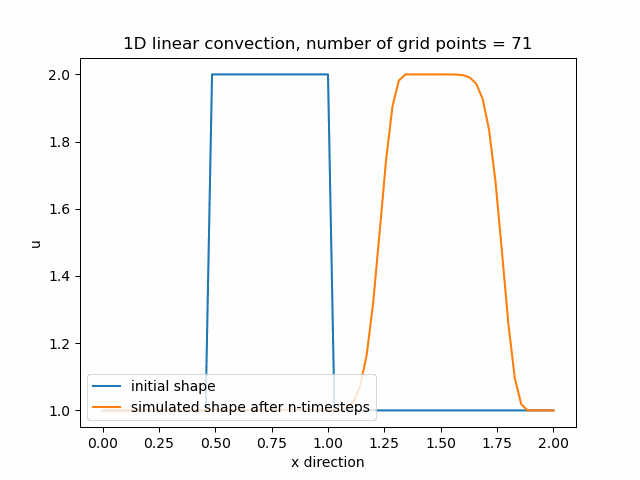
Průběh funkce pro nx=85, v tomto případě je zajemnění již příliš velké a funkce diverguje.
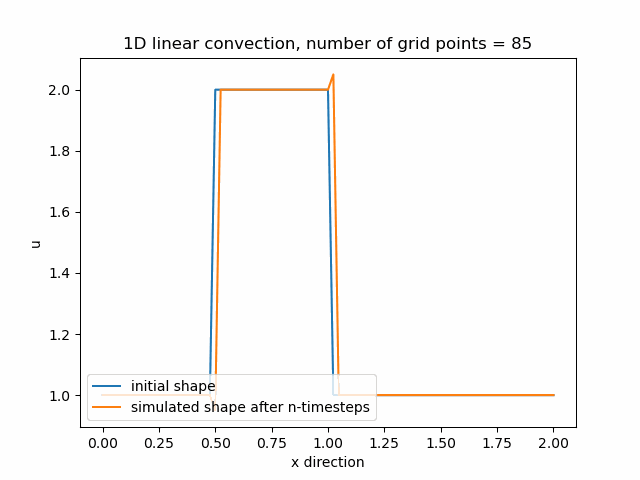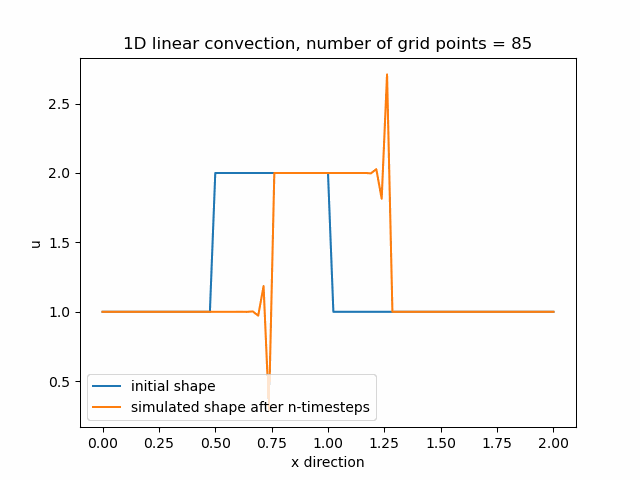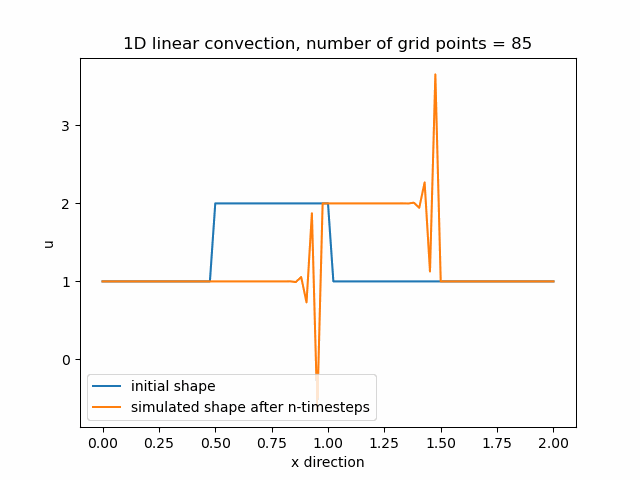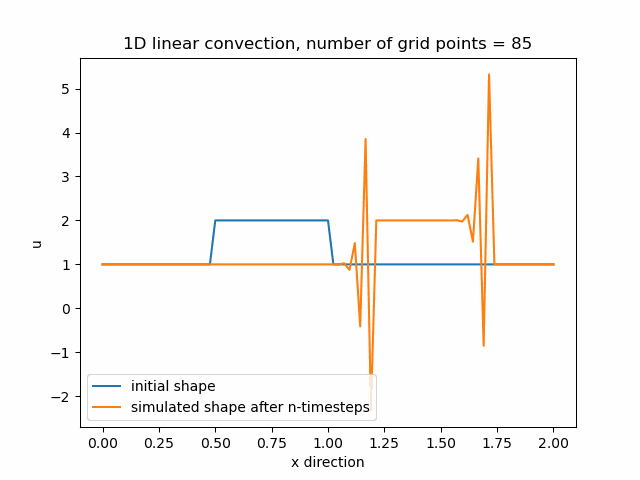
Z výše uvedených průběhů funkcí je tedy zřejmé, že čím více zajemňujeme výpočetní mřížku, tím menší je numerická difuze a získáváme přesnější výpočet.
Každá iterace se odehrává v délce časového kroku $\Delta t$, který je stanoven na hodnotu 0.025
V každé iteraci vypočítáme rychlost vlny pro všechny body $x$.
V případě, že byla hodnota nx nastavena na hodnotu 85 již ale nedošlo k dalšímu zmenšení difuze, ale funkce se nám "rozpadla". To je způsobeno tím, že vlna v čase $\Delta t$ urazila větší vzdálenost než dx. Tato vzdálenost je dána celkovým počtem bodů nx, proto stabilitu výpočtu můžeme vyjádřit následujícím vztahem:
$$ \sigma = \frac{u \Delta t}{\Delta x} \leq \sigma_{\max} $$
kde $u$ je rychlost vlny, $\sigma$ je tzv. Courantovo číslo, $\sigma_{\max}$ je maximální hodnota stability pro danou diskretizaci.
Do našeho původního kódu tedy implementujeme vzorec pro kontrolu stability výpočtu na základě CFL čísla, čímž určíme vhodný časový krok ve vztahu k potřebnému zajemnění.
sigma=0.5 #CFL number
dt = sigma * dxČasový krok se tedy bude měnit v závislosti na zajemnění mřížky výpočtu. Pokud bude CFL číslo menší než 1, výpočet bude stabilní. V příkladu je zvolena hodnota sigma=0.5. V následujícíh příkladech postupně zajemňuji mřížku, čímž se mění časový krok.
Časový krok pro nx=41 je dt=0.025.
Časový krok pro nx=61 je dt=0.017.
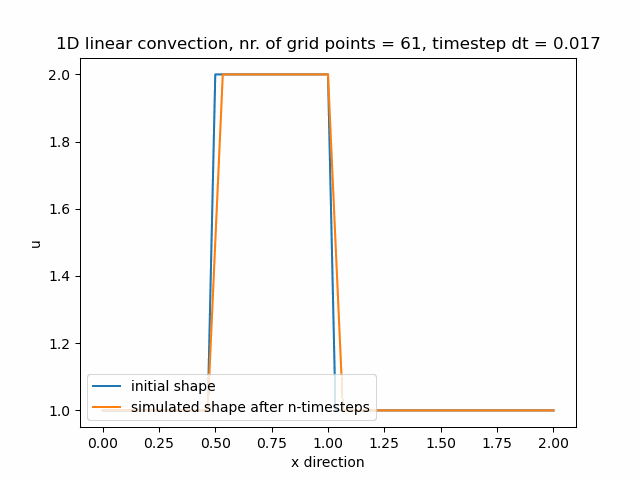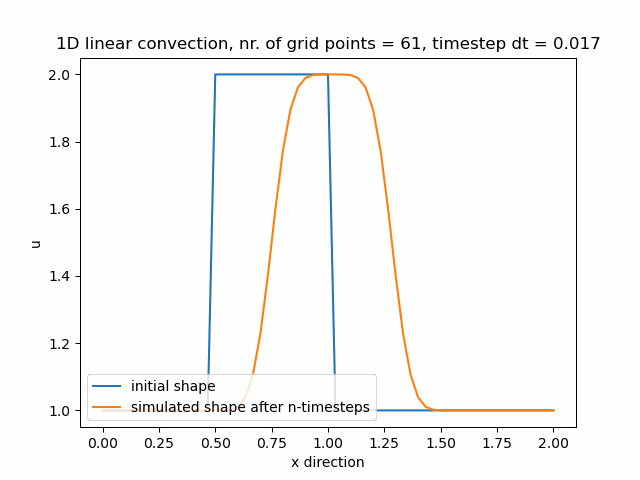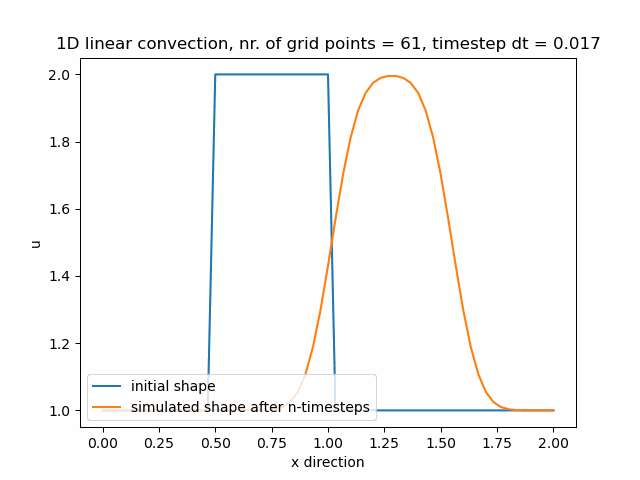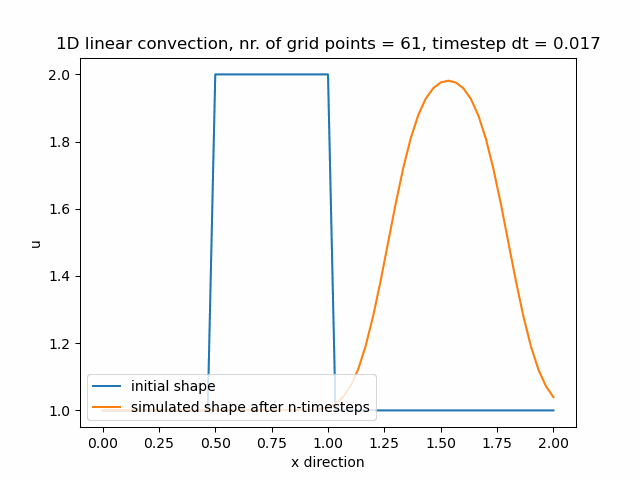
Časový krok pro nx=81 je dt=0.013.
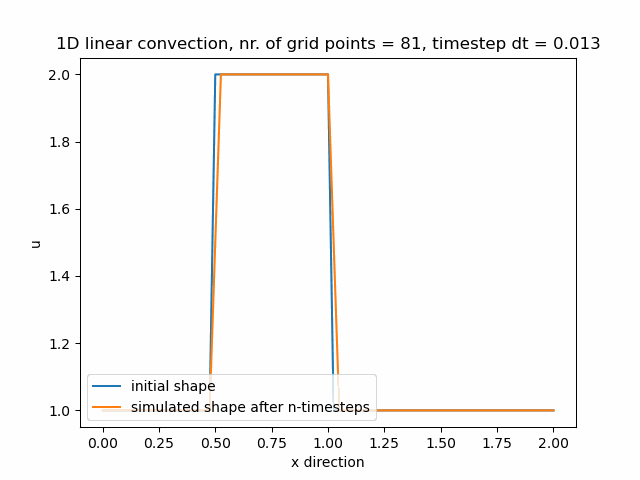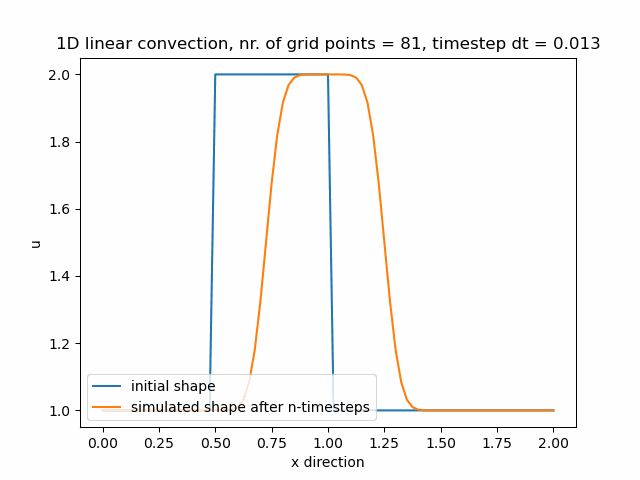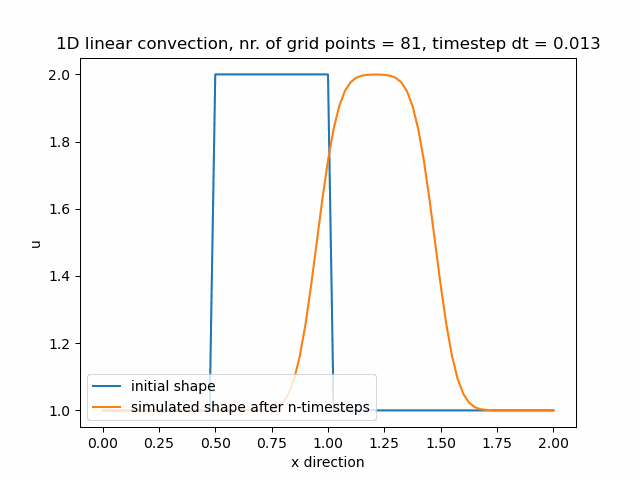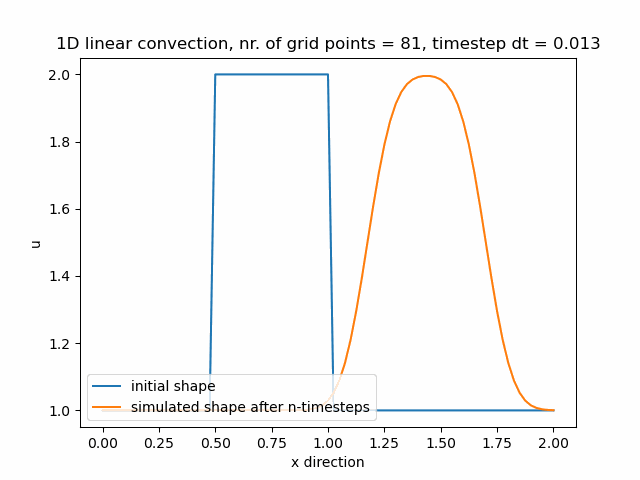
Časový krok pro nx=101 je dt=0.01.
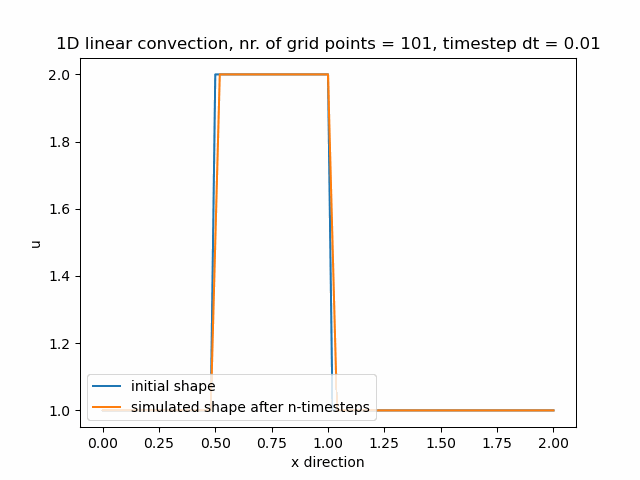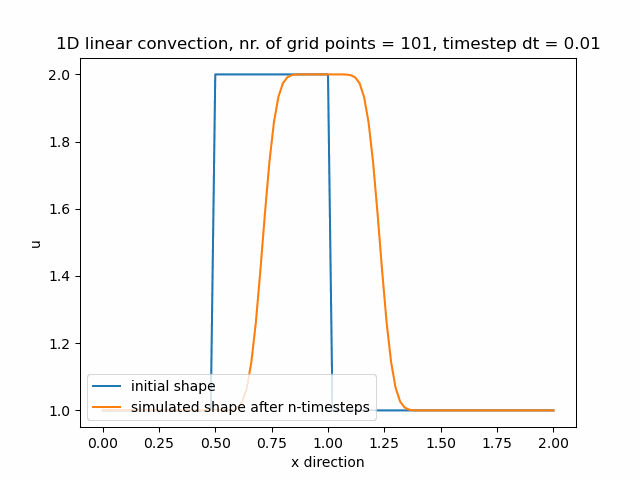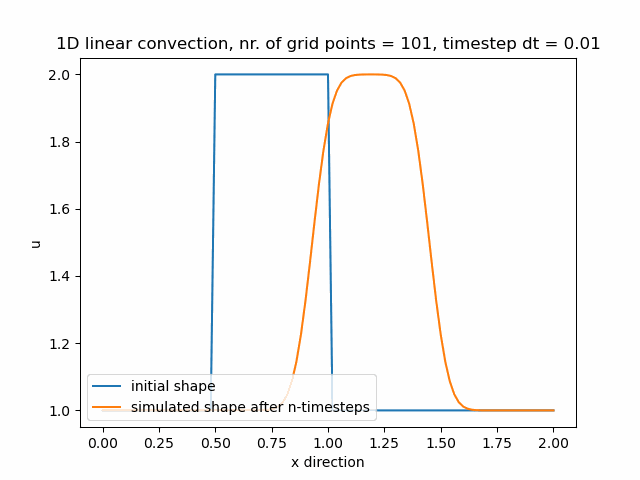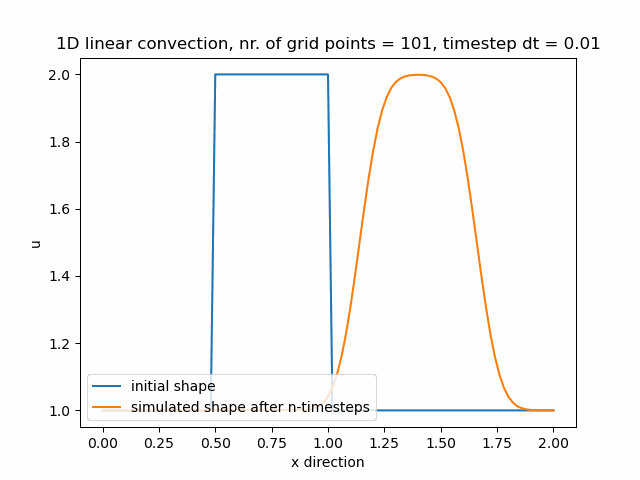
Časový krok pro nx=121 je dt=0.008.