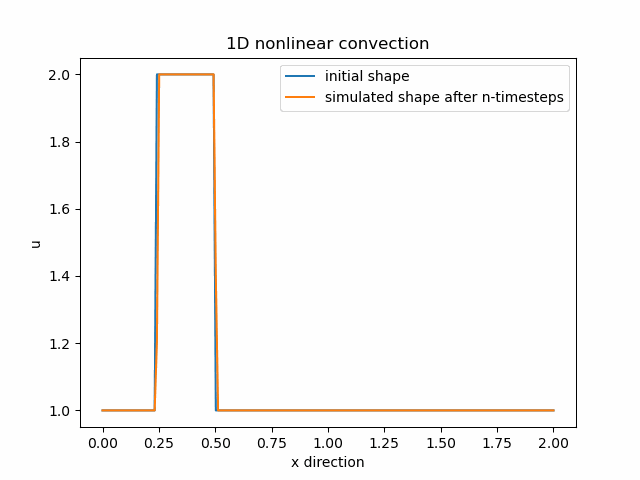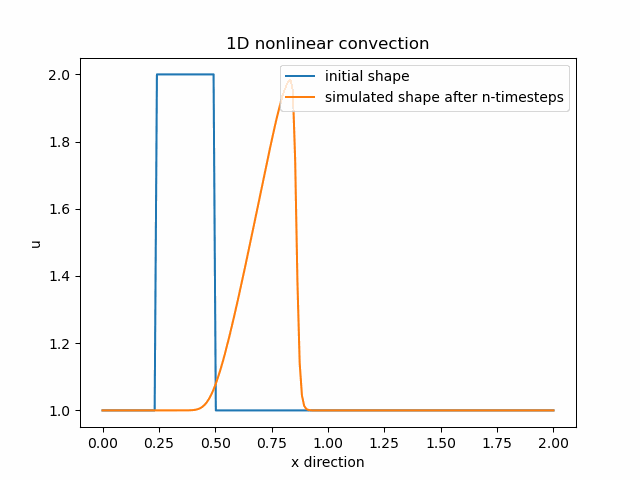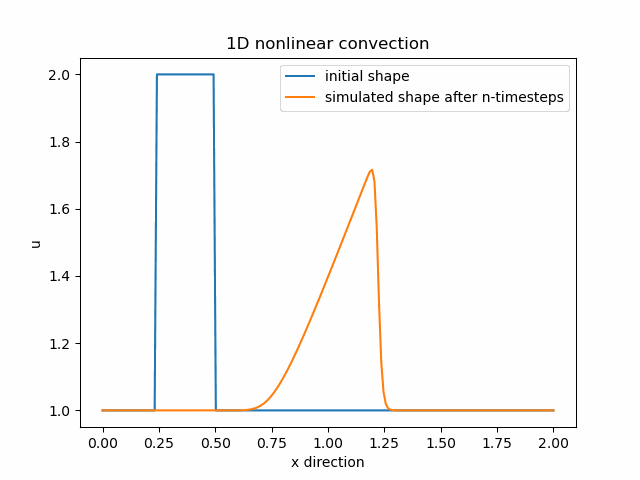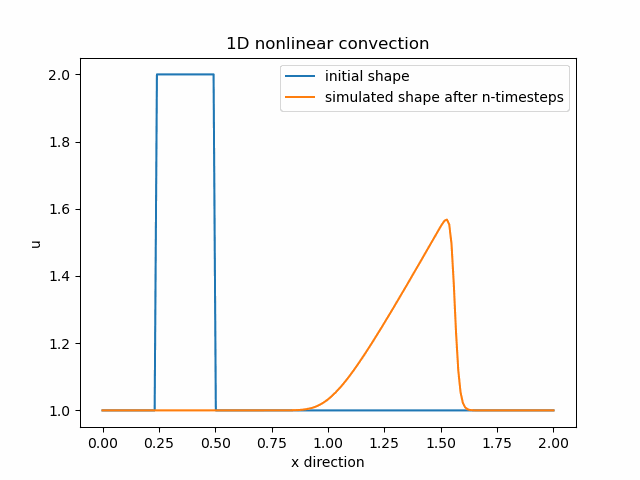
1D nelineární konvekce
V druhém kroku upravím původní kód tak, aby zahrnoval rovnici pro nelineární konvekci. Nelineární konvekce je podobná té lineární, liší se pouze v tom, že se nepohybuje konstantní rychlostí c, ale rychlostí u:
$$ \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = 0 $$
Okrajové podmínky nastavím např. takto:
nx=200 #number of grid points
dx=4/(nx-1) #distance between adjacent points
dt=0.008 #time of each timestep
nt=1 #number of timestepsDo výpočtu použijeme původní rovnici, pouze namísto konstantní rychlosti c, která násobí druhý výraz, dosadíme rychlost u. Nyní je náš druhý výraz nelineární. Použijeme stejnou diskretizaci – forward difference FD v čase a backward difference BD v prostoru:
$$ \frac{u_i^{n+1}-u_i^n}{\Delta t} + u_i^n \frac{u_i^n-u_{i-1}^n}{\Delta x} = 0 $$
Z této rovnice opět vyjádříme jedinou neznámou, čímž vypočteme následující krok v čase:
$$ u_i^{n+1} = u_i^n – u_i^n \frac{\Delta t}{\Delta x} (u_i^n – u_{i-1}^n) $$
Tuto rovnici opět implementujeme v kód jako iteraci časových kroků:
for i in range(1,nx):
u[i] = un[i] - un[i] * (dt/dx) * (un[i] - un[i-1])Pomocí knihovny Matplotlib opět získáme animaci chování naší funkce: