1D lineární konvekce
Jako první krok jsem napsal kód pro simulaci lineární konvekce v jednodimenzionálním prostoru.
Nejprve definujeme vstupní hodnoty proměnných:
u = np.zeros(nx) + 1 # setting the grid of zeros plus init value
u[int(0.5/dx):int(1/dx+1)] = 2 # setting interval 0.5-1 to value 2
uinit = np.zeros(nx) + 1 # setting the grid of zeros plus init value
uinit[int(0.5/dx):int(1/dx+1)] = 2 # setting interval 0.5-1 to value 2Poté stanovíme okrajové podmínky:
nx=80 #number of grid points
dx=4/(nx-1) #distance between adjacent points
dt=0.025 #time of each timestep
nt=1 #number of timesteps
c=1 #wave speedZákladem je nejjednodušší základní model CFD vycházející z rovnice:
$$
\dfrac{\partial u}{\partial t}+c\dfrac{\partial u}{\partial x} = 0
$$
Pro diskretizaci této funkce použijeme schéma FD (Forward difference) derivované v čase a BD (Backward difference) derivované v prostoru. Tímto získáme diskretizační rovnici:
$$
\frac{u_i^{n+1}-u_i^n}{\Delta t} + c \frac{u_i^n – u_{i-1}^n}{\Delta x} = 0
$$
$n$ a $n+1$ jsou dva po sobě jdoucí kroky v čase. $i-1$ a $i$ jsou dva sousední body ve směru $x$. Z této rovnice vyjádříme neznámou $u_i^{n+1}$, čímž získáme následující krok v čase:
$$
u_i^{n+1} = u_i^n – c \frac{\Delta t}{\Delta x}(u_i^n-u_{i-1}^n)
$$
Takto upravenou rovnici použijeme přímo v kódu jako iteraci časových kroků:
for n in range(1,nx):
u[n] = un[n] - c * (dt/dx) * (un[n] - un[n-1])Nakonec pomocí knihovny MATPlotLib vygenerujeme animaci postupného chování naší funkce:
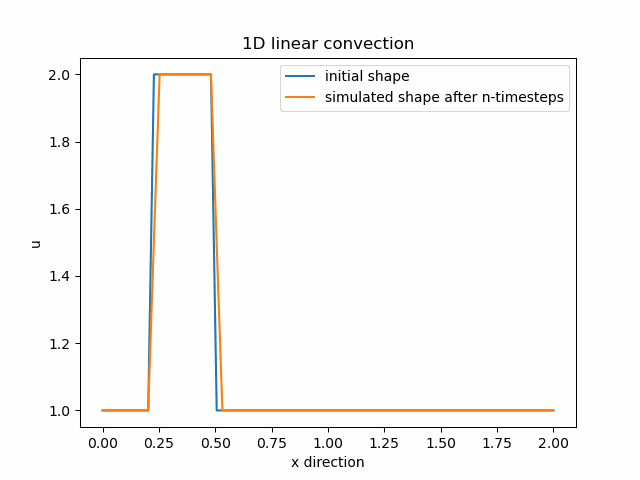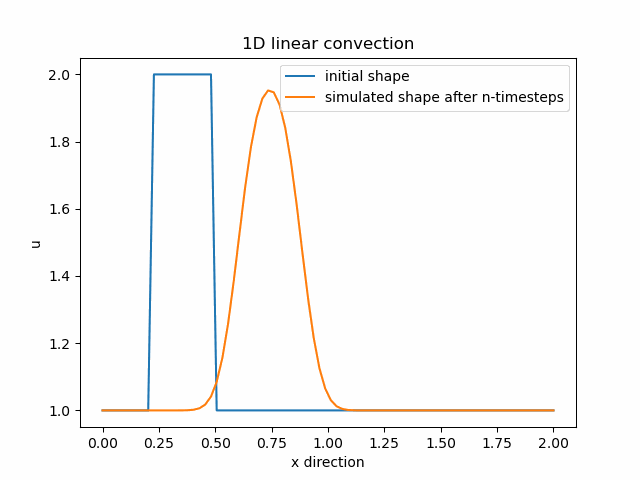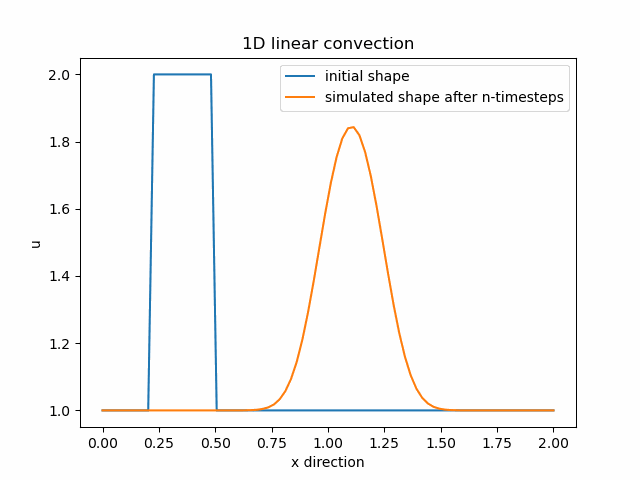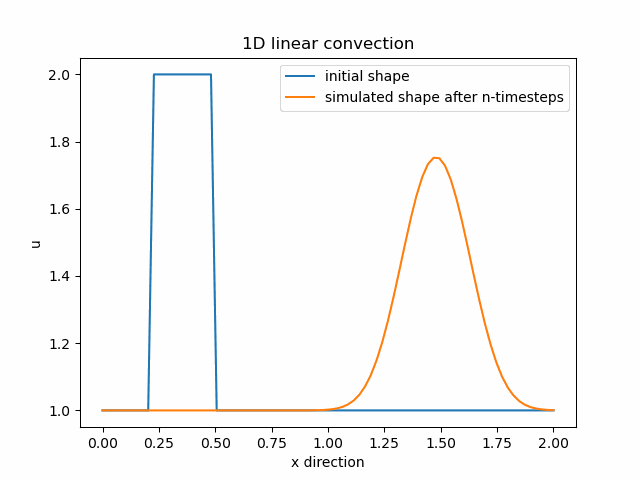
V animaci vidíme, že v průběhu šíření vlny postupně aproximací ztrácíme informaci o naší funkci. Řešením je zmenšení vzdálenosti jednotlivých diskretizovaných bodů dané funkce.
nx=160 #number of grid points